Multi-Armed Bandits

The Multi-Armed Bandit is one of the classic problems studied in probability theory and AI and it’s one of the first problems you are likely to look at when doing a Reinforcement Learning class. The basic premise is that you have a row of one-armed bandit machines, each tuned to pay out a reward based on a different random variable. When playing you have to decide between choosing to play with the bandit that you think will give you the highest reward, and playing with another bandit which will allow you to build up a more accurate picture of the rewards available.

This trade-off between exploration and exploitation can be seen in many real-world scenarios and research on advanced versions of the Multi-Armed Bandit problem is still ongoing nearly seventy years after the problem was first explored.

For more background information see the Wikipedia Article.

Goal

Write an AI that learns then selects the bandit which returns the highest reward.

Algorithms and Hints

Create an AI that either picks a random bandit, or chooses the bandit that has returned the highest average reward. Select which of the two strategies to use for each pull based randomly (based on a percentage). This is known as the e-greedy algorithm.
Alter the algorithm so that all of the random pulls are taken first.

Setup

At the start of each round, each bandit is assigned a different random variable with a normal distribution N(μ,σ²).

The following options are available when setting up the scenario:

# Bandits	The number of bandits available, numbered 0…n-1.
# Pulls	The number of arm-pulls in each round.
Bandit Mean	How the mean of each bandit is chosen
Bandit Standard Deviation	How the standard deviation of each bandit is chosen
Update Rule	How the mean of each bandit is updated after each step
Random Salt	A repeatable salt for the random number generator – use ‘0’ to create a new value each time
Skip intermediate frames	If checked the screen (and output) will only be updated at the end of each round, rather than after every pull. This dramatically reduces the amount of time spend updating the UI.

API Interface

The Swagger specification for this API can be downloaded here.

In each step the Sandbox Client will send the following to the AI server:

history – the result of the last step (except for the first step of the first round), this consists of:
- sessionID – the session identifier for the previous step
- chosenBandit – the index of the bandit selected by the AI
- reward – the reward from the chosen bandit.
sessionID – a session identifier, this will stay constant for the entire round.
banditCount – the number of bandits available (numbered 0..n-1)
pullCount – the number of times the bandits arm can be pulled in a round
pull – the number of pulls already made this round

Note: If the number of pulls in a round is 100, then the pull parameter will range from 0 to 99.

JSON Example Request

{
  "history": {
    "sessionID": "DEF-5435",
    "chosenBandit": 4,
    "reward": 1.42
  },
  "sessionID": "ABC-23542342",
  "banditCount": 10,
  "pullCount": 10000,
  "pull": 0
}

JSON Example Response

{
  "arm": 3
}

XML Example Request

<?xml version="1.0" encoding="UTF-8"?>
<BanditRequest>
	<history>
		<sessionID>DEF-5435</sessionID>
		<chosenBandit>4</chosenBandit>
		<reward>1.42</reward>
	</history>
	<sessionID>ABC-23542342</sessionID>
	<banditCount>10</banditCount>
	<pullCount>10000</pullCount>
	<pull>0</pull>
</BanditRequest>

XML Example Response

<?xml version="1.0" encoding="UTF-8"?>
<BanditResponse>
	<arm>3</arm>
</BanditResponse>

Graphical Output

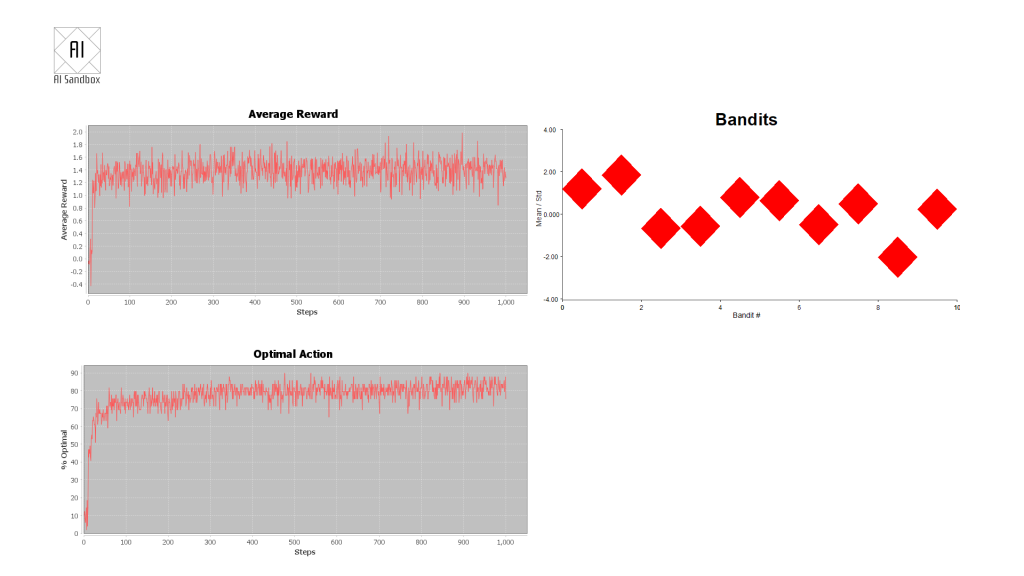
The graphical output shows three charts:

Average reward – the reward from each step of the round, averaged over all rounds.

Optimal action – the average percentage that the AI picks the best bandit (the bandit with the highest mean value) at each step in the round.

The current mean (centre of each diamond) and standard deviation (top and bottom of each diamond) of each of the bandits.

Statistics Output

The statistics file will show the average reward and the amount of times each step has chosen the best answer, averaged over all rounds.


Step	Ave Reward	% Optimal Action
0	0.11180486767982283	8.0
1	-0.16001485097160476	6.000000000000003
2	0.01309801032724169	6.000000000000001